📍 Goal of the Competition
"The goal of this competition is to compute smartphones location down to the decimeter or even centimeter resolution, which could enable services that require lane-level accuracy such as HOV lane ETA estimation. Your work will help produce more accurate positions, bridging the connection between the geospatial information of finer human behavior and mobile internet with improved granularity. As a result, new navigation methods could be built upon the more precise data." Kaggle challenge page
The training data is from 62 separate drives around San Francisco and the Los Angeles area. Navigation Satellite Systems (GNSS) Data, Inertial Measurement Unit (IMU) Data were collected from 1-5 phones during each drive. In addition, the ground truth data were collected from a high-precision GNSS-IMU device in the exact vehicle. The map below shows the traces of the ground truth and the baseline obtained from the GNSS data.
The submissions are evaluated with a separate test dataset. The score is the mean of the 50th and 95th percentile distance errors for every phone and second. The 50th and 95th percentile errors are then averaged for each phone. Lastly, the mean of these averaged values is calculated across all phones in the test set.
🌍 The Coordinate Systems
Before we begin with the GPS data, let's talk about the coordinate systems used in this project. Choosing the correct coordinate system for each function and accurately converting the different coordinate systems are crucial in this project. The four coordinate systems used in this project are:
- Earth-Centered Earth-Fixed(ECEF) coordinate system
- Geodetic coordinate system
- Scene East-North-Up (ENU)
- Car-centered
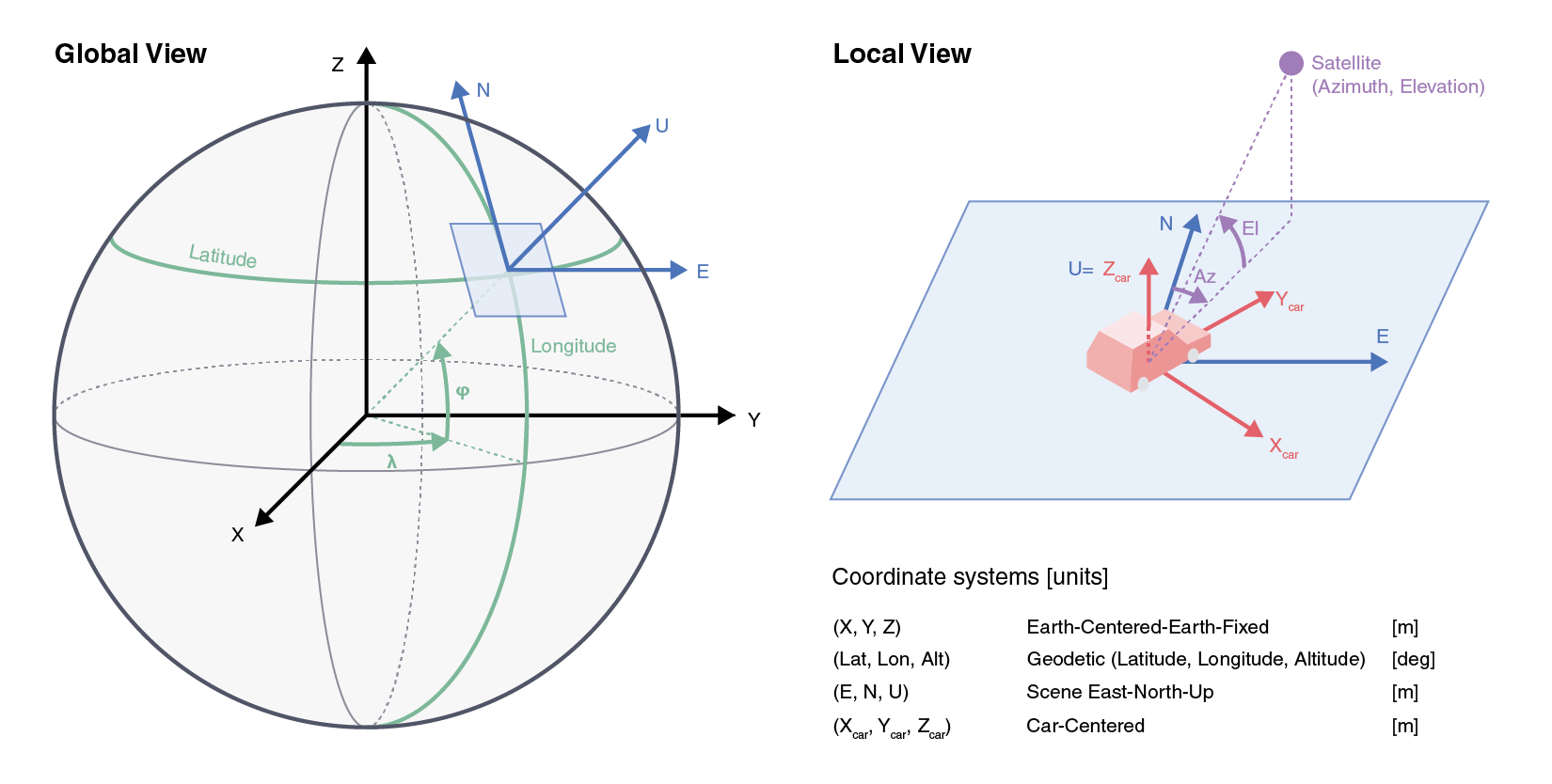
Earth-Centered Earth-Fixed(ECEF) coordinate system
First, the satellites are tracked with the ECEF coordinate system, also called the Geocentric coordinate system. The interactive plot below shows the location of the GPS satellites in this dataset compared to the Earth. The origin is at the center of the chosen ellipsoid, which in this case is the Earth's center of mass.
- The X-axis is the line through the origin and the prime meridian in the plane of the equator.
- The Y-axis is the line through the 90E and 90W longitude planes and the equator's plane.
- The Z-axis is the line between the North and South Poles.
Geodetic coordinate system
Geodetic coordinate system is a spherical coordinate system where longitude and latitude define the angles from the reference axes, and the altitude is defined as the distance from the origin.
Scene East-North-Up (ENU)
The scene ENU coordinate system only applies in a relatively small area since it approximates the Earth's curved surface into a local plane. The x, y, and z axes are the directions East (+x), North (+y), and Up (+z). Care should be taken when this coordinate is used since the error between the actual location and the location in this ENU approximation increases are the device travels far from the origin.
Car-centered coordinate system
You are in your own universe when driving. In this universe, you are always moving forward as the world revolves around you. The y-axis is always aligned with the driving direction (heading), and the x-axis is always on the side of the car.
📡 How does GNSS work?
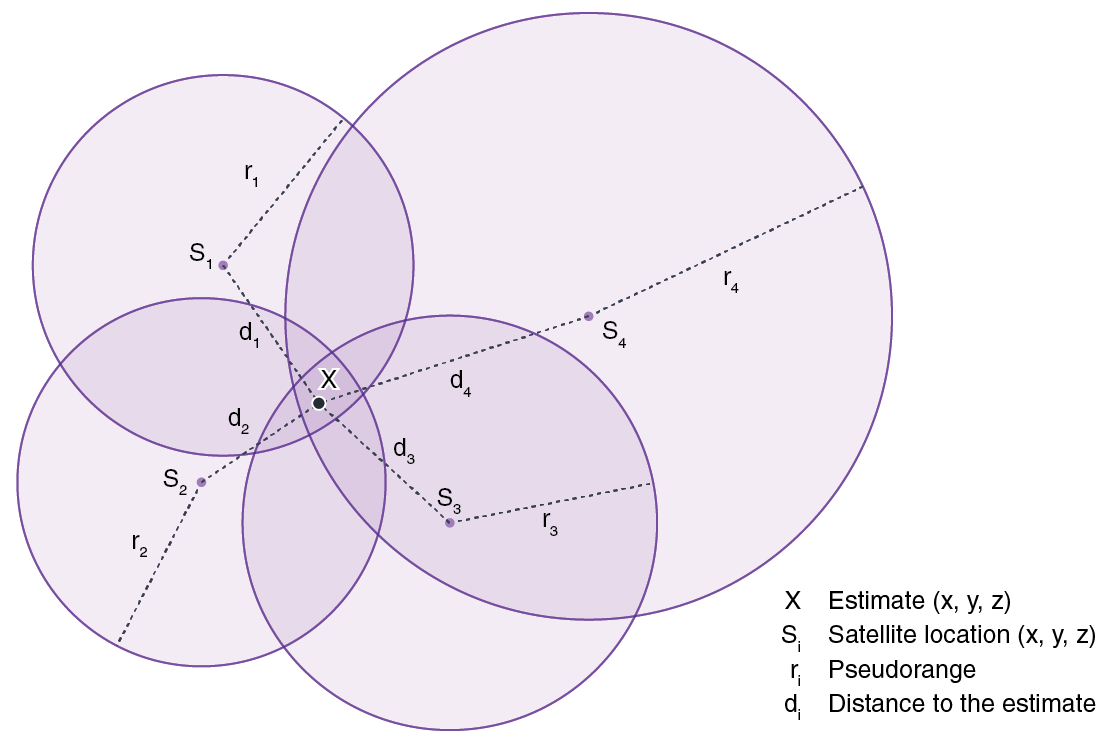
Global Navigation Satellite System (GNSS) uses satellite information to provide positioning of small devices. Among the GNSS systems, the US government-owned Global Positioning System (GPS) is used in the United States. The location of the 30+ GPS satellites is known at any given time. These satellites constantly send signals, which are received from mobile GNSS/GPS devices. The elapsed time from the satellite's transmission to reception is used for calculating the distance between the device and the satellite.
The location of the device can be triangulated (or 'trilateration') when the distance to at least four satellites is available. Due to the errors in satellite signals, however, the location can only be estimated using optimization. GPS locations are generally estimated using a Weighted Least Squared (WLS) technique. When the satellite locations are Si, the location X is where the weighted sum of the squared error Σ(ri - di)2 is minimal.
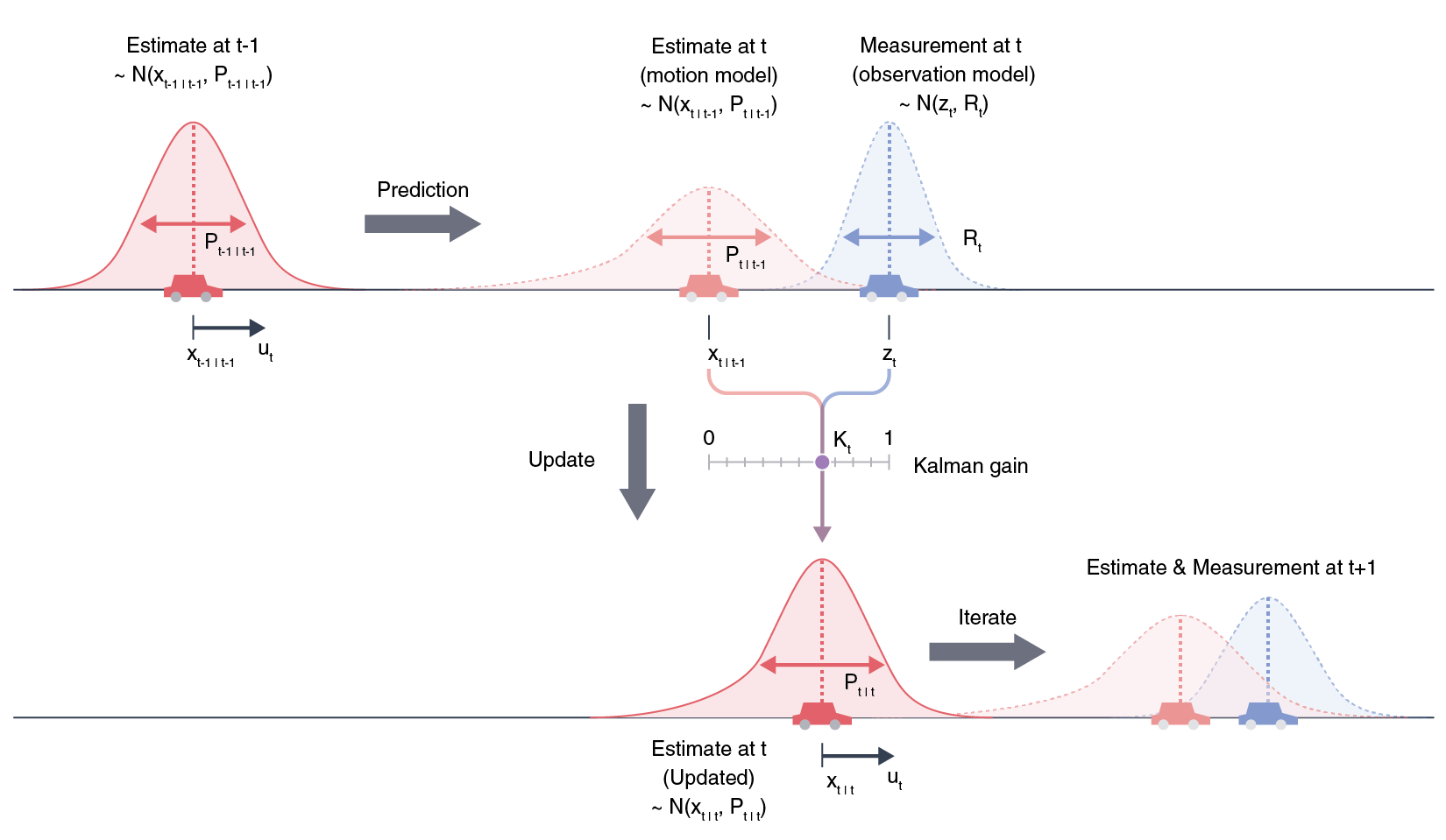
🪄 Kalman Filter
In this project, the Kalman filter is used to reduce the errors. Kalman filter is an optimal estimation method that uses both a prediction model based on the previous state and a new measurement to optimize the state of the next step. For GPS positioning, the prediction is the physical model based on the position and velocity of the device, and the measurements are from the satellites' GNSS data.
- First, the state is initialized with the position and velocity at the time 0. The position xt-1|t-1 is assumed to have a Gaussian distribution with a variance of Pt-1|t-1, where t-1 denotes the time of the "previous step".
- Next, an estimation xt|t-1 is made based on the state at t = t-1. This estimation is assumed to have a Gaussian distribution, and the variance of the estimate (Pt|t-1) is derived from the previous step.
- The next measurement zt is obtained, which also has a Gaussian distribution with a variance Rt. The measurement, however, is not necessarily at the same location as the model prediction.
- The next estimation Pt|t is therefore calculated by combining the information from the model and the measurement. The weight of the model in this calculation is the Kalman gain Kt, and it depends on the uncertainty of the model and the measurements.
- This process is iterated to make the next estimations.
👨🔧 The "Advanced" Kalman Filter
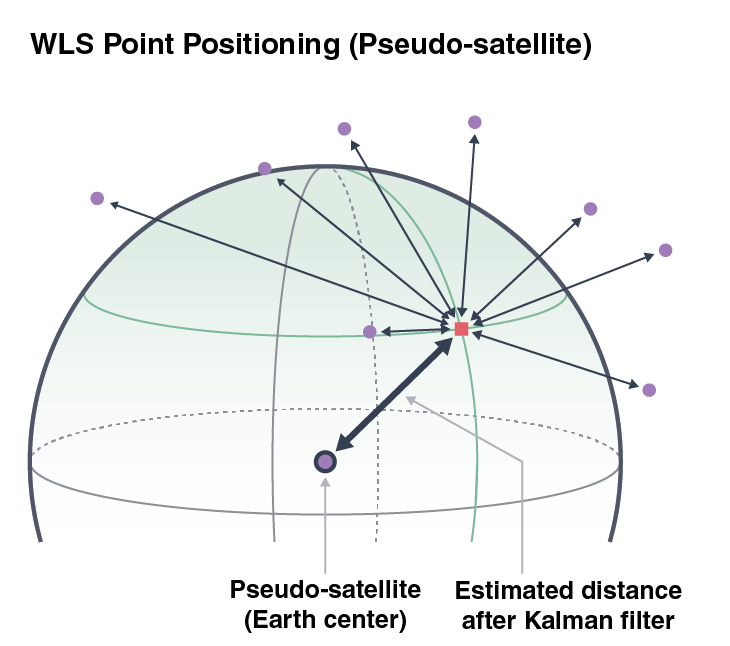
Pseudo-Satellite Estimation
Several new approaches to the GNSS positioning was implemented in order to advance the Kalman Filter. Here, we introduce two of the new approaches used for the submission.
The approximated locations of the device during the trip is obtained with the Kalman filter. This new approximation could also be used in the point positioning optimization process.
If we think that there is a satellite at the center of Earth (hence, pseudo-satellite estimate), we can use the distance to the Kalman filter estimate as a new pseudorange.
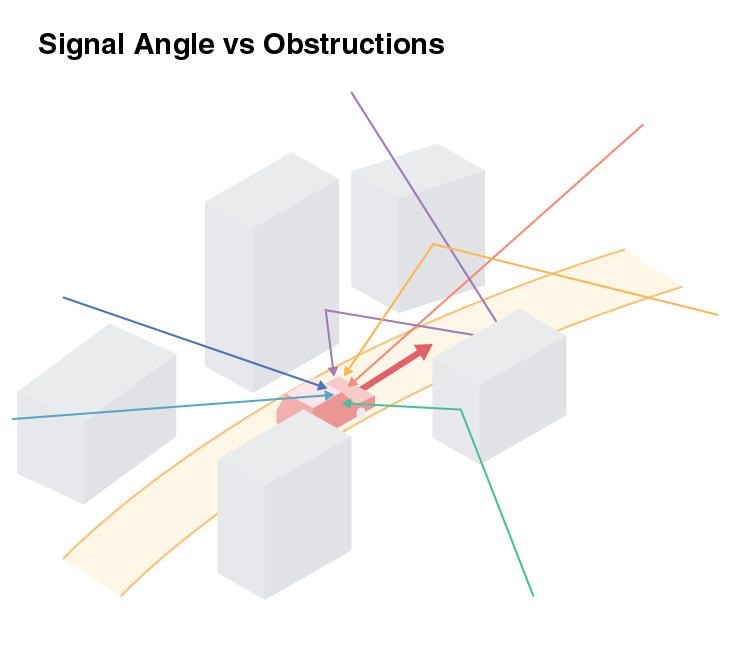
Signal Angle Penalization
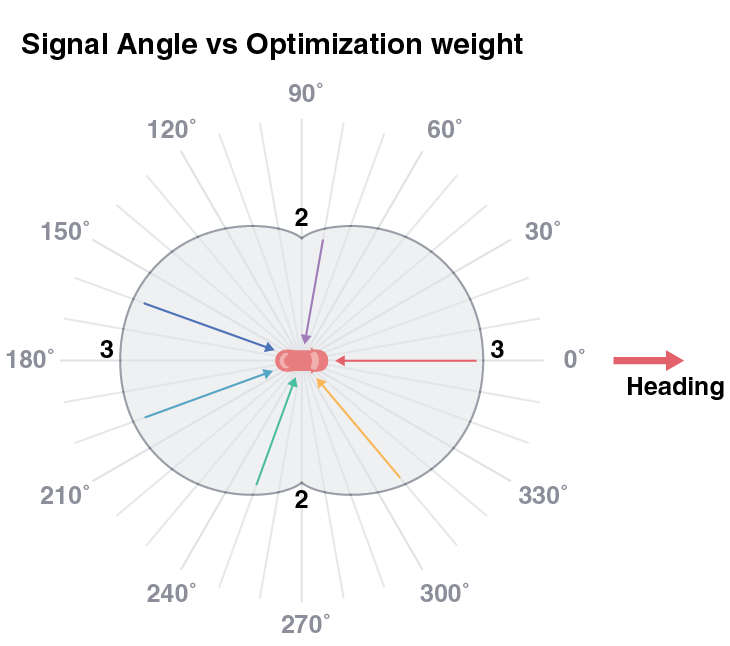
Obstructions are one of the significant sources of GPS errors, and signal reflects on objects, adding error to the transmission time. Since the data is collected during drives, we can assume that there are more obstructions on the car's sides (x-axis in the car-centered coordinate system) than along the driving direction (y-axis in the car-centered coordinate system). We can multiply the weight in the WLS optimization by 2+abs(cos(angle)) to penalize the signals from the sides.
🎖️ Results
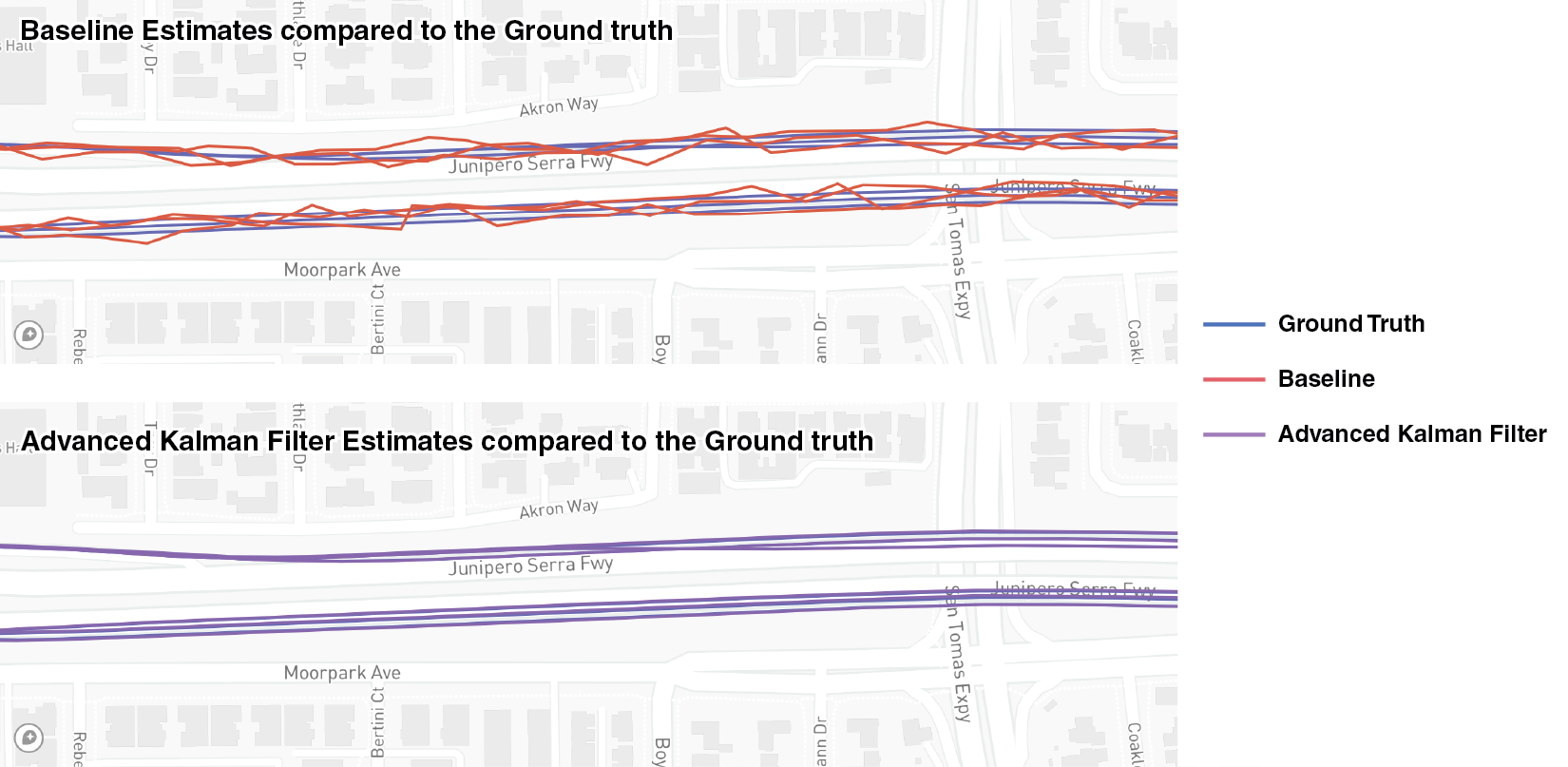
Comparison with the baseline
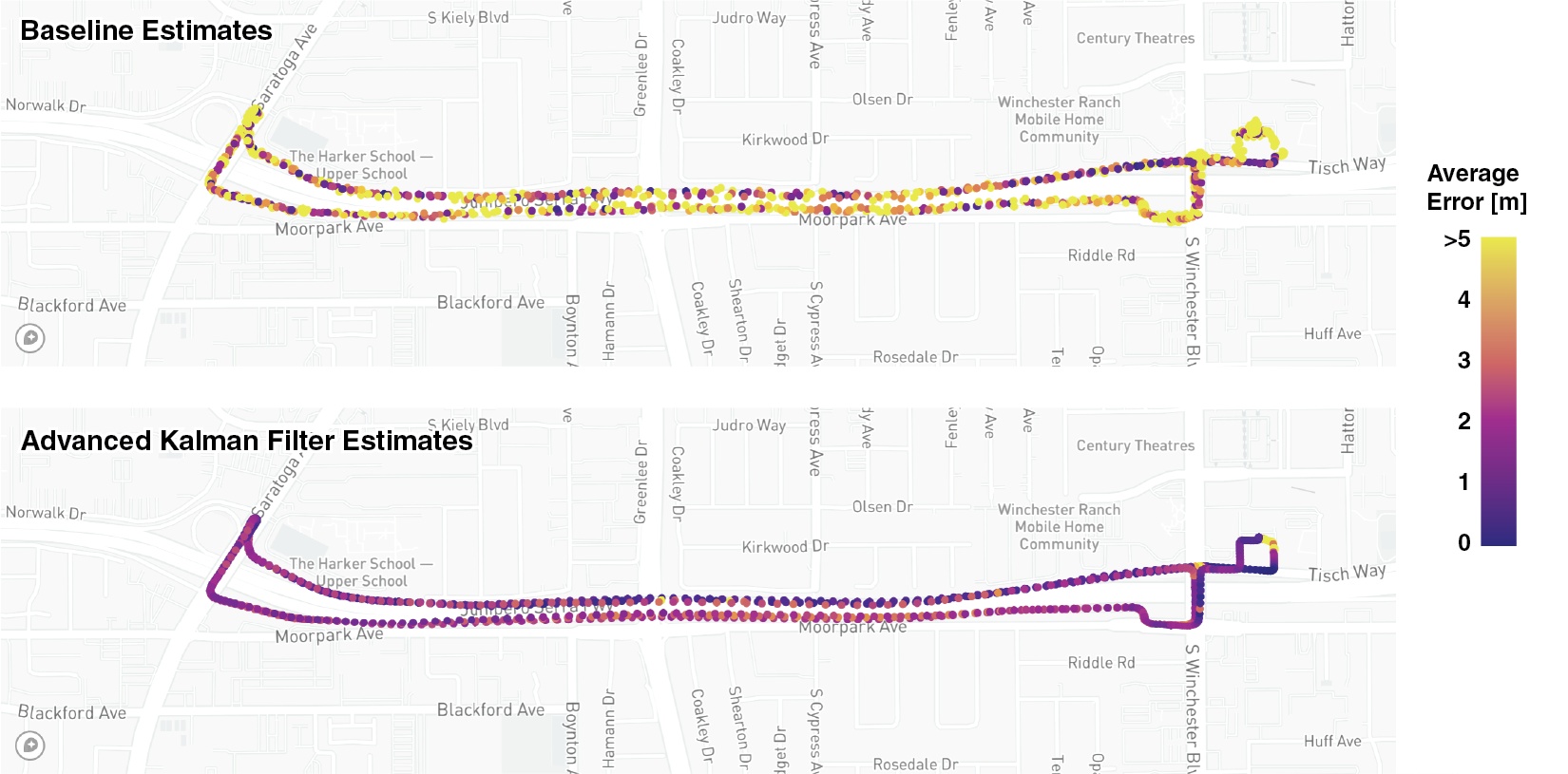
The baseline, Kalman Filter, and Advanced Kalman Filter estimates are visualized below. The errors from the Ground truth were: Baseline 9.24 m, Kalman Filter 3.46 m, and Advanced Kalman Filter 2.70 m. You can zoom in to the center of the map to see how accurately the Kalman Filter can estimate where the device is, which even successfully differentiated which lane the car was driving on.
The two plots below compare the errors of the baseline and advanced Kalman filter estimates. Any datapoint with an error larger than 5m is shown in yellow. We can clearly see that most of the points have an GPS error lower than 5 meters after the Kalman filter.
Finally, the distribution of the errors are plotted as density plots. The baseline errors were much larger with many outlier datapoints. After the WLS optimization, Kalman filter, and the advanced Kalman filter, the error has significantly decreased.
📝 Current Status
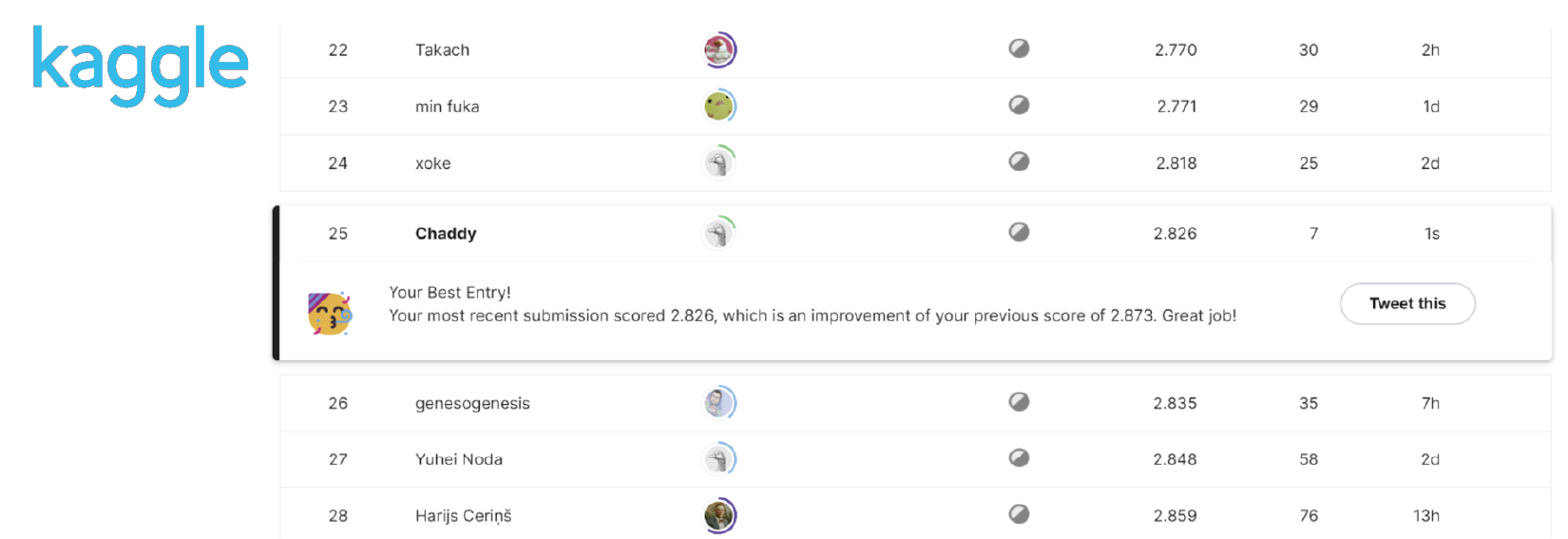
We successfully implemented WLS optimization, Kalman Filter, and more advanced and creative techniques to reduce the GPS error. The results are submitted to Google Decimeter Challenge (Kaggle), and the current score of this method is 2.826 m, with a current ranking of 26th as of June 22nd, 2022. This is already a 42% error reduction from the baseline 🥳
This project is developed by Chad Loh, Layal Hammad, Michelle Bui, and Caroline Keough
Data Source
- Fu, Guoyu (Michael), Khider, Mohammed, van Diggelen, Frank, "Android Raw GNSS Measurement Datasets for Precise Positioning," Proceedings of the 33rd International Technical Meeting of the Satellite Division of The Institute of Navigation (ION GNSS+ 2020), September 2020, pp. 1925-1937. DOI
- Fu, Guoyu (Michael), Khider, Mohammed, van Diggelen, Frank, (2022, May), Google Smartphone Decimeter Challenge. Retrieved [Date Retrieved] from Link.